The Chaos Game
Awhile back, I watched a YouTube video on something called the "Chaos Game". This "game" could take random dice rolls and a simple rule and create a fractal. I found the video fascinating and have linked it here, but I wanted to take it a step further and actually generate my own fractals.
The Game
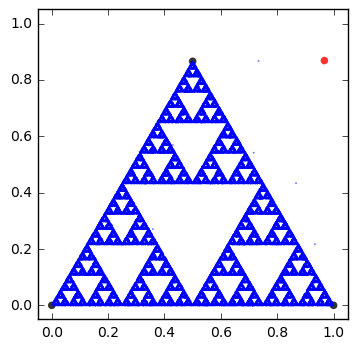
In order to play the game, like any game, there are some rules you must follow.
- First, you draw three points.
- Next, you label these points so that they correspond to the rolls of a 6-sided dice e.g: (1,2),(3,4),(5,6).
- Then you draw a fourth point, this is your starting point.
- Now the game begins, roll the dice and make a point halfway between the starting point and the point corresponding to the number you rolled.
- From that new point, roll the dice again and place a point halfway between it and the point you rolled.
Unbelievably, if you continue this process for long enough, you obtain an image like the one above.
More Fractals
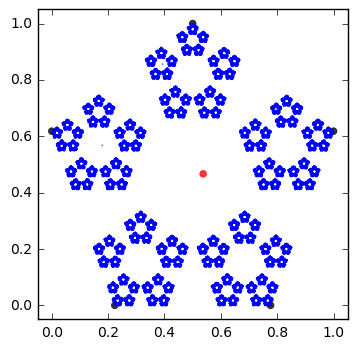
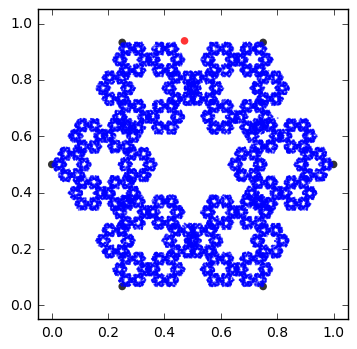
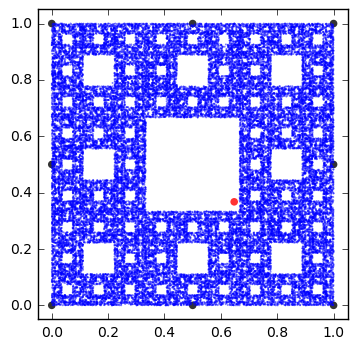
I then took the game a few steps further and made it so that you weren't limited to three points placed randomly, but instead you could place many points. I also changed the rules so that instead of halfway between the points, maybe you only went a third of the way or maybe a quarter. The results were incredible.
The key to this game it turns out is the math of something called "attractors" and in fact these fractals are just a few of these mathematical objects. For more about how I generated these images, checkout my GitHub page.
Modeling Life
Nature is full of fractals, just looking outside, trees are a great example. A tree has a central trunk, that trunk then splits into branches, the branches into smaller branches, those into even smaller branches and eventually leaves, themselves containing a central vein and several layers of smaller branching veins. This natural "self-similarity" is most easily modeled using fractal mathematics.
Here I created a fractal known as Barnsleys fern. The code to generate it can be found here.